The Makings Behind Tic Tac Toe

Agents

The agents in our system would be those that are participating in our game of Tic Tac Toe. Therefore we have two agents, the user and the AI. In order to manage the agents within my code, I had to created several objects to store information about the agents that were initialized through the modal setting option. I made several utility function throughout my object in order to ease the process of retrieving and maintaining the state of these agents

Below is a code snippet that shows how I am able to store information about the agents within the game:

    let agents = {

        userIcon: '',

        aiIcon: '',

        init: function () {
            this.userIcon = $('input[name=icon]:checked').attr('id')[0];
            this.aiIcon = this.getOpponent(this.userIcon)
        },

        getOpponent: function (player) {
            if (player === "X") {
                return "O";
            }
            return "X";
        },

        getPlayerIcon: function (player) {
            if (player === "user") {
                return this.userIcon;
            }
            return this.aiIcon;
        },
    };

States

To represent the states of the problem, I had to create a model that allows us to imitate that of a tic tac toe turn. This would subsequently result in a model that contains information about the current board, the current turn as well as any other necessary information relevant to the current state of the game. To represent the board, I used a 2D array where each index contains an array that represents the row on a tic tac toe board. The position's indices are based on a (X,Y) coordinate system where the top left most position corresponds to a value of (0,0). X's and O's were placed onto the game board based on when they were inserted during the game. The board is initially initialized with "-"which corresponds to blank spots on the board.

For the sake of keeping this as abstracted as possible, I've remove code within my functions below. If you're interested in viewing the implementatio, I would encourage that you visit the repository source code [insert repository after cloning]. Below is a code snippet of how I formulated the state of the game :

    let gameState = {
        sessionTime: 0,
        currentTurn: '',
        gameBoard: [],
        openPositions: [],
        winningCombos: [],


        init: function () {
            this.currentTurn = gameSetting.startingTurn;
            let initialState = this.createInitialGameState();
            this.gameBoard = initialState.board;
            this.openPositions = initialState.openMoves;
            this.winningCombos = this.getWinningStates();
        },

        createInitialGameState: function () {
            // Created an object that contains an array of the initial board as well
            // as the remaining open positions on the board
        },

        getWinningStates: function () {
            // Given the initial dimensions of the board, calculate and return an array
            // that contains all the possible winning combinations
        }
    };

Operator

In the rules defined by the game, valid moves are only allowed where there's an empty position within the current game board for a marker to be placed at. Thus, you need a function to check whether a position is empty, prior to carrying out some action. For our game, a function that checks whether a position is open is relatively straight forward, given that we are already keeping track of the current state of the game. To make the process much easier for myself, I created an operator function that utilizes the rules set forth by the game and returns an array of legal game boards for that current state.

Below is a snippet of the getSuccessors function:

    function getSuccessors(board, nextMove) {
        let successors = [];
        for (let i = 0; i < dimension; i++) {
            for (let j = 0; j < dimension; j++) {
                let boardTemp = JSON.parse(JSON.stringify(board));
                if (boardTemp[i][j] === "-") {
                    boardTemp[i][j] = nextMove;
                    successors.push(boardTemp);
                }
            }
        }
        return successors;
    }

Actions

The actions in our game are made when an agent decides to place a marker at a position on the game board. If the actions is legal, verified by the operator, then the action can be carried out and thus will change the internal and external state of the game. Since the action of the user is triggered through the user interface, we have to change the internal state of the game. Actions generated by the AI is done internally and uses an algorithm called minimax (which will be discussed below) and thus must result in a change in the user interface.

Below is a code snippet that manages the action taken by the user and AI and changes the internal and external state of the game:

    function makeMove(position) {
        let pieceId = "#position-" + position;
        let arrayPosition = getBoardPosition(position);
        gameBoard[arrayPosition.x][arrayPosition.y] = getPlayerIcon(currentTurn); // Changes internal game board
        removeFromArray(openPositions, position);
        if (getPlayerIcon(currentTurn) === "X") {
            if ( currentTurn === "user") {
                currentTurn = "ai";
            } else {
                currentTurn = "user";
            }
            $(pieceId).append($('<span class="fa fa-times times-symbol"></span>')); // Changes external game board
            $(pieceId).off('click');
        } else {
            if ( currentTurn === "user") {
                currentTurn = "ai";
            } else {
                currentTurn = "user";
            }
            $(pieceId).append($('<span class="fa fa-circle-o circle-symbol"></span>')); // Changes external game board
            $(pieceId).off('click');
        }
    }

Standard Evaluation Function

When making our decision on a particular action, we want to be able to weigh the effectiveness of said action based on the consequences of that action. We need a way to know the benefits of each action relative to each other in order to make the best decision. This requires that we have some way to capture relative effectiveness. This is typically best done so through a function that is able to capture the state of game after an action has been carried out in order to measure the effectiveness of that action.

In my case, I used a standard evaluation function that measures the effectiveness of a board relative to one of the three terminal state in our game; the AI winning, the user winning and a tie. I awarded game boards that resulted in the AI winning, 10 points, states that resulted in the user winning, -10 points and those with ties, 0.

Below is a snippet of the implementation of the scoring function:

if (gameStatus !== false) {
    switch (gameStatus) {
        case 1:
            return {
                score: 10 - depth,
                board: board
            };
        case 0:
            return {
                score: 0,
                board: board
            };
        case -1:
            return {
                score: -10 + depth,
                board: board
            };
        }
    }
}

MiniMax Algorithm

Now that we have been able to formulate the current system in which we are in, we can now discuss how we are able to utilize these formulations in order to make optimal decisions. To be able to make the most optimal decision, we need to somehow know the effectiveness of our actions. In formulating our problem, we mentioned an evaluation function as a means to measure the effectiveness of certain actions. With there being so many combinations of actions that can occur within a system, we need to be able to generate all of these potential states that are a result of these actions and then evaluate them on their effectiveness. To do so, we will be introducing the MiniMax algorithm.

The MiniMax algorithm is a backtracking algorithm that utilizes recursion to be able to explore potential states in order to find the most optimal move for a particular agent. This is done so by assigning what are called min and max to the corresponding agents within the system. The idea behind MiniMax is that while generating potential states, we are utilizing a scoring function that also assigns a value to those newly generated states in order to measure their effectiveness. The agent assigned to min will want to minimize the score from an evaluation function, while max will do it's best to maximize the score. Due to the recursive nature of this algorithm, we are able to continually generate potential states until no more actions are allowed. This will then invoke a backtracking process that will be able to return the most optimal state based on our evaluation function.

Below is an image of the recursive process that generates actions in the MiniMax algorithm.

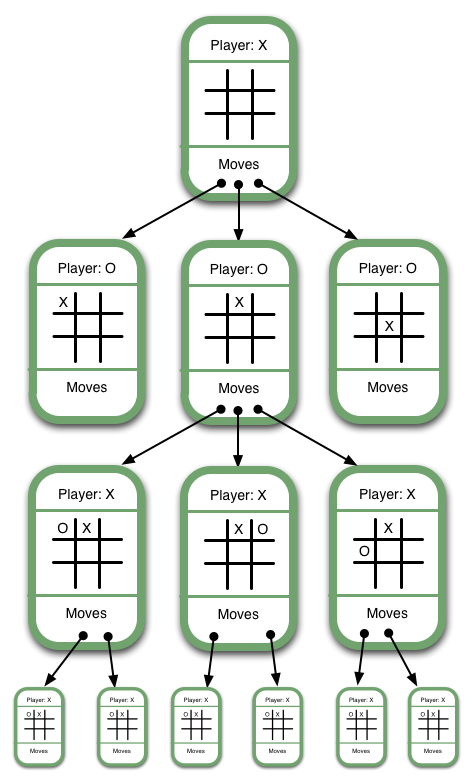
Tic Tac Toe Game Tree from Swarthmore CS

Utilizing the MiniMax algorithm, we are able to analyze potential actions now and see how they play out in the future. This idea is incredibly powerful in the sense that it helps illustrate the process behind generating an optimal decision in a strategic setting.

Closing Notes

Although there is a lot more to game theory than what was mentioned, I hope that this serves as a solid foundation into some of the concepts behind game theory. These concepts extends beyond simple games and artificial systems. Due to the nature of how our society is shaped, decisions play an essential role in everything we do. Being able to understand the context surrounding our decisions allows us to act intelligently in order to achieve some kind of goal. I would encourage anyone who is interested in these concepts to further explore the domain as a lot of the underlying principles behind game theory parallels that of how our world works.

Currently in the Works

I am currently in the process of optimizing my code in order to support Tic Tac Toe games of 4x4 and 5x5 dimension boards. Currently my code will still work but the time that it takes to generate the next optimal state takes too long and thus is ineffective and derails the game experience. I have thus disabled those options until a future update. I have done a bit of additional research and planning on steps that are needed to be able to optimize my code. Below are some of the techniques that I will attempt to implement in order to be able to cut down my runtime.

• Alpha Beta Pruning
• Zobrist Hashing
• Memoizing Function Calls
• Better Static Evaluation Function

For any suggestions and or comments, feel free to reach me here

Follow my progression at { insert repo after cloning it as my own repo }